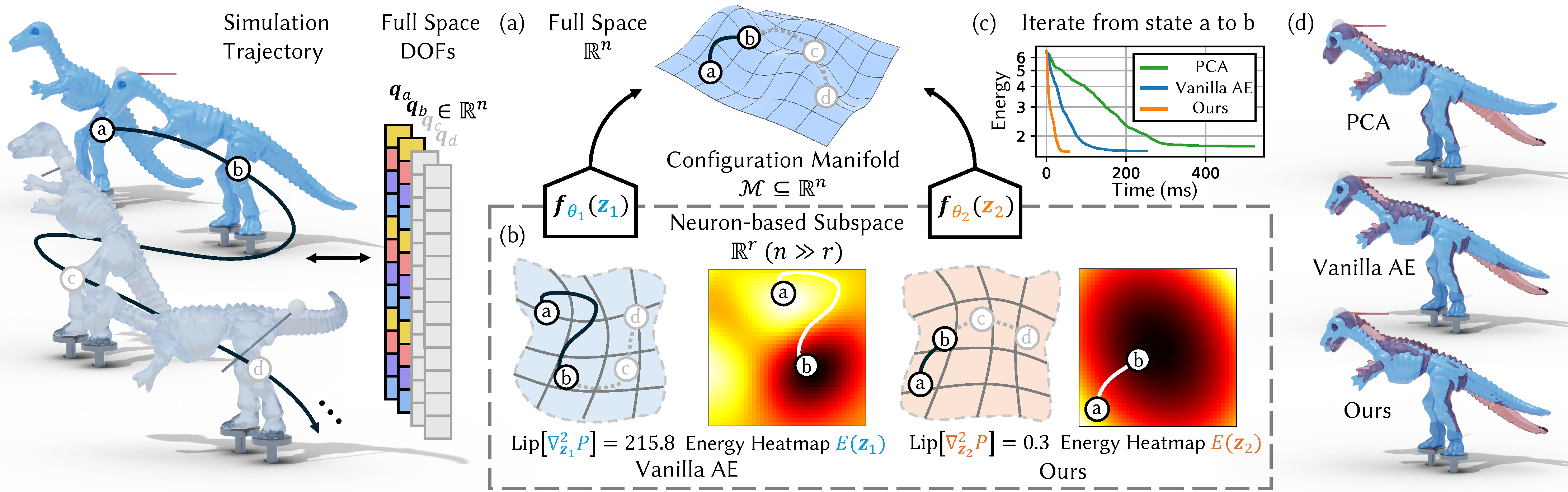
Accelerate Neural Subspace-Based Reduced-Order Solver of Deformable Simulation by Lipschitz Optimization

SIGGRAPH Asia 2024 (ACM Transactions on Graphics)

Aoran Lyu1, 3, *, Shixian Zhao1, *, Chuhua Xian1, †, Zhihao Cen1, Hongmin Cai1, Guoxin Fang2, †
1.South China University of Technology, China
2.The Chinese University of Hong Kong, China
3.The University of Manchester, United Kingdom
* Equal contribution of the first two authors
† Corresponding authors (Email: chhxian@scut.edu.cn, guoxinfang@cuhk.edu.hk)
arXiv Video Code (release after conference) Data (coming soon)

This paper introduces a Lipschitz optimization method that can significantly accelerate the convergence speed of reduced-order simulations driven by neural-network-based approaches. (a) The deformation process can be formulated as a path through a configuration manifold \(\mathcal{M} \subseteq \mathbb{R}^n\), where reduced-order solvers tend to find a mapping \(f_\theta(z)\) that maps a low-dimensional subspace \(\mathbb{R}^r\) to the manifold. (b) Our method enhances the objective landscape in the neural subspace by minimizing the second-order Lipschitz regularization energy, which substantially improves convergence speed when using iterative solvers like Newton's method. (c, d) Compared to conventional linear subspace methods (driven by PCA) and direct neural subspace constructions, our method achieves faster convergence and maintains quality when using the same subspace dimension.

Abstract

Reduced-order simulation is an emerging method for accelerating physical simulations with high DOFs, and recently developed neural-network-based methods with nonlinear subspaces have been proven effective in diverse applications as more concise subspaces can be detected. However, the complexity and landscape of simulation objectives within the subspace have not been optimized, which leaves room for enhancement of the convergence speed.

This work focuses on this point by proposing a general method for finding optimized subspace mappings, enabling further acceleration of neural reduced-order simulations while capturing comprehensive representations of the configuration manifolds. We achieve this by optimizing the Lipschitz energy of the elasticity term in the simulation objective, and incorporating the cubature approximation into the training process to manage the high memory and time demands associated with optimizing the newly introduced energy. Our method is versatile and applicable to both supervised and unsupervised settings for optimizing the parameterizations of the configuration manifolds. We demonstrate the effectiveness of our approach through general cases in both quasi-static and dynamics simulations.

Our method achieves acceleration factors of up to 6.83 while consistently preserving comparable simulation accuracy in various cases, including large twisting, bending, and rotational deformations with collision handling. This novel approach offers significant potential for accelerating physical simulations, and can be a good add-on to existing neural-network-based solutions in modeling complex deformable objects.

Video

Overview

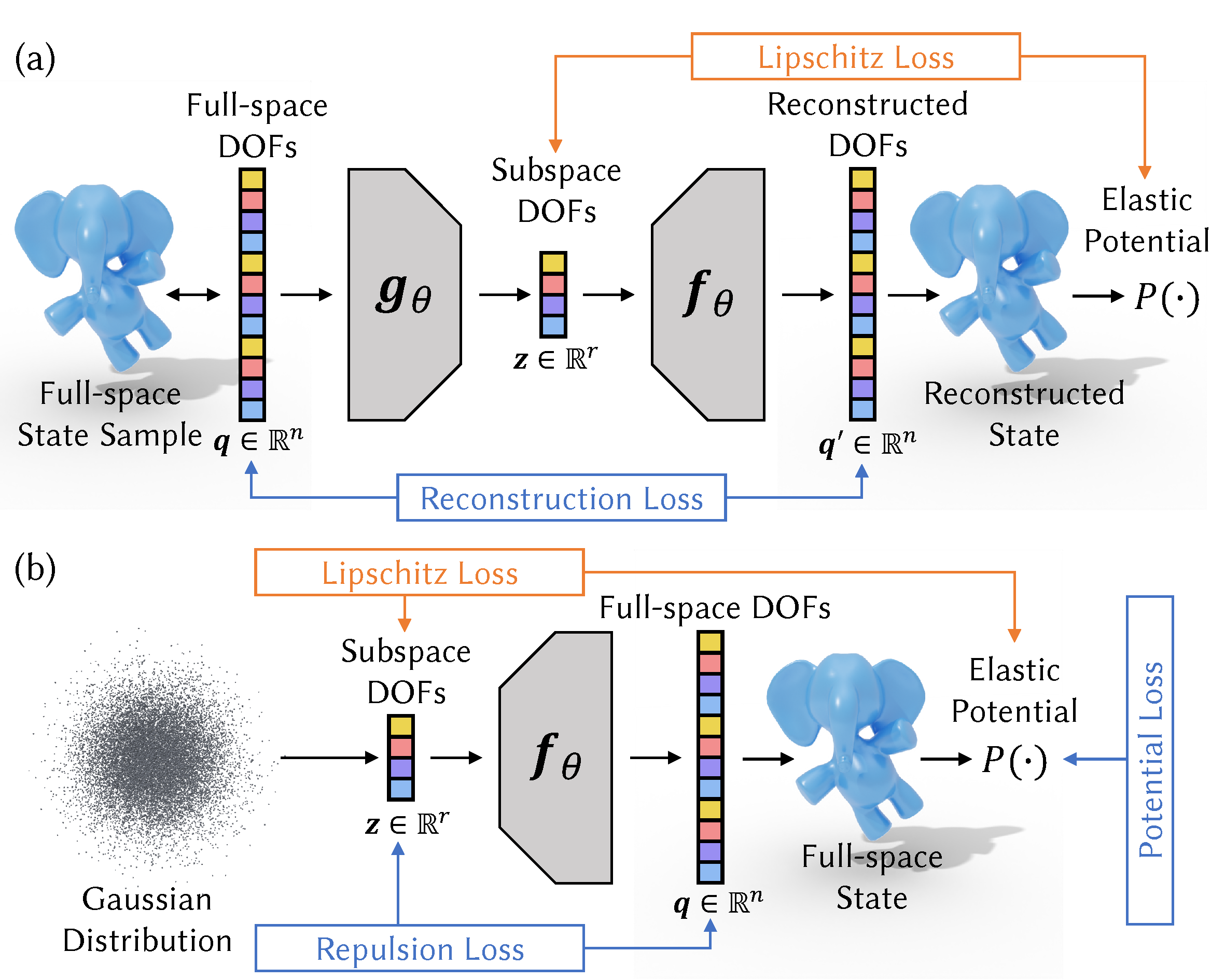
An overview for our neural subspace construction settings. (a) The supervised setting. (b) The unsupervised setting. Conventional methods only consider the construction losses shown in blue but do not optimize the Lipschitz loss (shown in orange) to control the landscape of the simulation objective in the subspace.


Experiment results

Quantitative Comparison on Simulation Speed

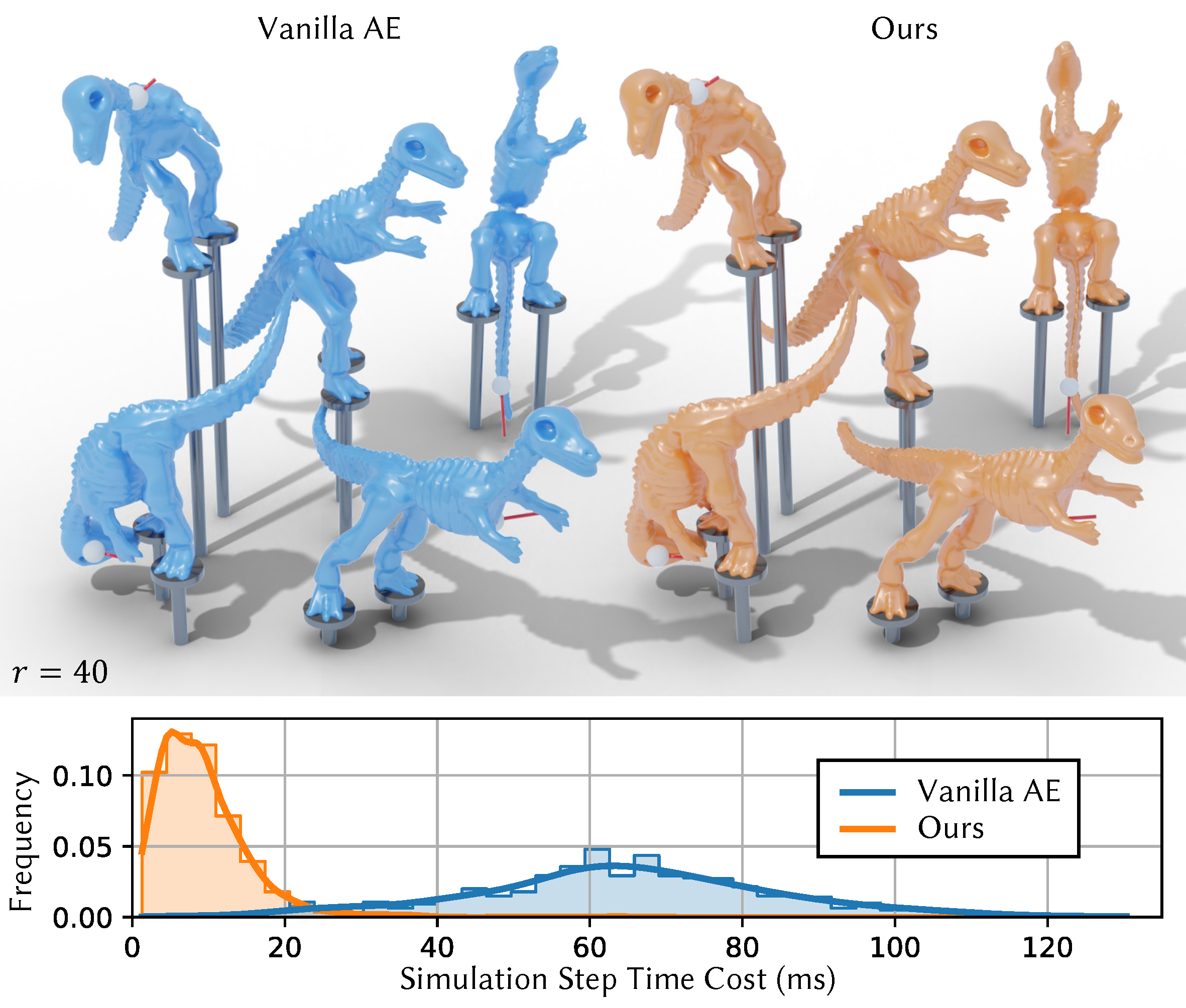
We compare the simulation speed of method and the vanilla subspace construction by collecting the simulation time cost distribution of the two methods. For the dinosaur example that produces complex deformations by applying interactions, our method reaches an acceleration rate of 6.83x.


Quantitative Comparison on Simulation Quality

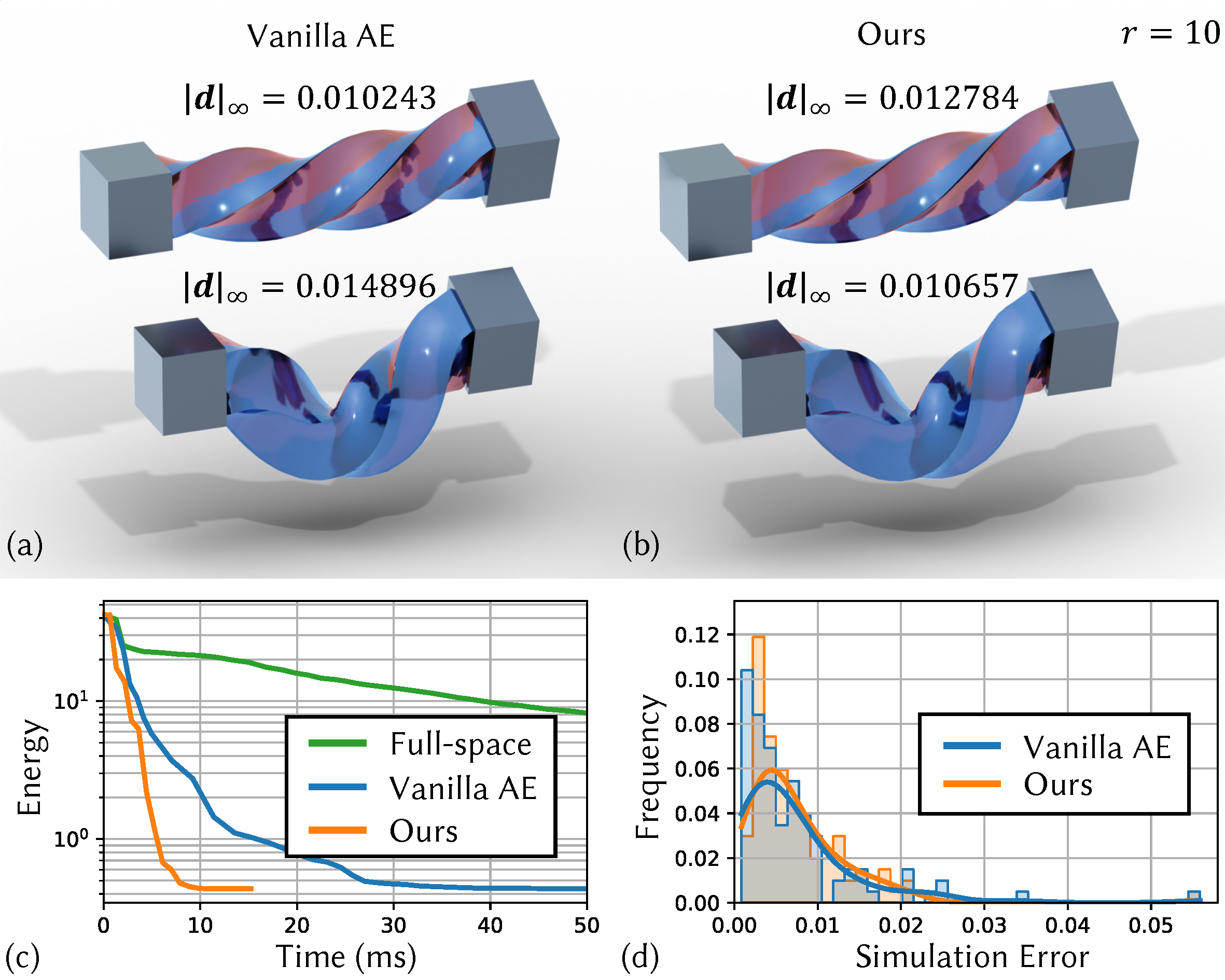
We compare the simulation quality of method and the vanilla subspace construction. (a) Results of vanilla neural subspace. (b) Results of our method with optimized Lipschitz energy. (c) For the shown simulation, the two methods converge to the same level of potential energy while the convergence speed of our method is accelerated by \(\sim\)3 times. (d) Simulation error distribution with full-space simulation as the reference. The solid lines are Kernel Density Estimation (KDE) plots that visualize the estimated probability density curves of the simulation error. The KDE of our method is analogous to that of the vanilla neural subspace construction, showing a comparable simulation quality of our method.


Influence of Subspace Dimension on Simulation Quality and Speed

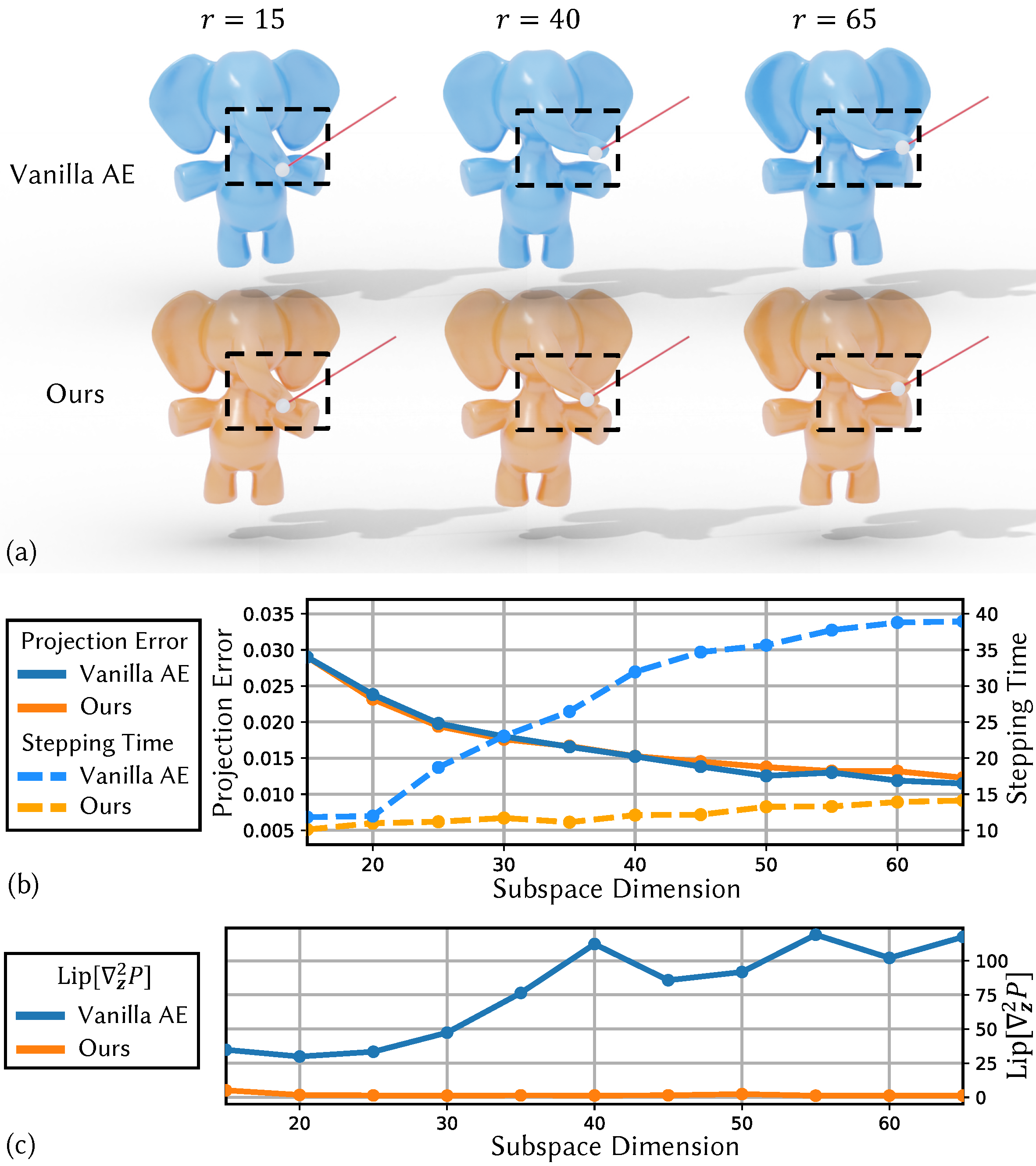
We construct subspaces of different dimensions for the Elephant example and compare their simulation quality and speed. (a) Qualitative comparison on simulation quality by applying a fixed interaction to the trunk. (b) Qualitative comparison on simulation quality and speed by mean error of full-space simulation states projections and mean simulation step time cost. (c) Qualitative comparison on the Lipschitz constants of the subspace Hessian. With the increase in the subspace dimension, our method demonstrates greater acceleration compared to the vanilla method because our simulation time remains small, while the vanilla method experiences a significant increase. This illustrates that our method can effectively enhance simulation quality by increasing the subspace dimension with only a small increase in simulation time.


Other experiments

We test the performance of the proposed Lipschitz optimization method in various physical systems and demonstrate that our method can effectively improve the Lipschitz constant of the subspace potential Hessian, resulting in simulation speedups. Furthermore, our method conserves subspace quality, thus achieving similar configuration manifold coverage and comparable simulation quality (please refer to our paper and supplemental video for all results).


BibTeX

Comming soon